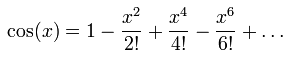
Bron: http://nl.wikipedia.org/wiki/Taylorreeks
.
© Harry Broeders.
Deze pagina is bestemd voor studenten van de Haagse Hogeschool - Academie voor Technology, Innovation & Society Delft.
Bij het vak GESPRG krijg je regelmatig een opdracht die als volgt begint: Schrijf een programma dat ... Hoe pak je zoiets (als beginnend programmeur) nu aan? Op een andere webpagina leg ik uit hoe je de volgende opdracht aanpakt: schrijf een programma dat een geheel getal 0 < n < 7 inleest en vervolgens de tafels van 1 t/m n naast elkaar afdrukt. Ik raad je aan om dat voorbeeld eerst te bestuderen! Op deze webpagina leg ik uit hoe je de volgende opdracht aanpakt: benader cos(x) met de volgende formule cos(x) = 1 - x2/2! + x4/4! - x6/6! + ... In deze formule is x de hoek in radialen waar je de cosinus van wilt benaderen en betekent "4!" 4 faculteit. Het aantal termen dat gebruikt moet worden om de cosinus te benaderen is variabel en moet door het programma worden ingelezen.
De methode die ik gebruik om tot een werkend programma te komen dat aan de opdracht voldoet is stapgewijze verfijning (Engels: stepwise refinement). Ik begin met een eenvoudig programma en breid het programma stap voor stap uit tot ik uiteindelijk het gewenste programma heb. Ik test het programma na elke stap. De bovenstaande opdracht zou ik als volgt aanpakken.
De eerste stap heeft nog niets met programmeren te maken. Voordat ik begin te programmeren denk ik eerst over de opdracht na. De formule waarmee de cosinus benaderd kan worden is dus:
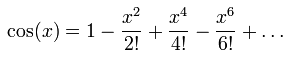
Bron:
http://nl.wikipedia.org/wiki/Taylorreeks.
In de opdracht wordt gespoken over "termen" en "faculteit". Als ik deze begrippen
niet ken dan zoek ik ze op. Volg indien nodig deze links:
termenen
faculteit. Ik stel mezelf de vraag hoe ik
in C xn uit kan rekenen. In de index van mijn C
boek
(De
programmeertaal C, 4e vernieuwde editie van Al Kelley en Ira Pohl, ISBN
9789043016698) vind ik dat machtsverheffen op pagina 25 wordt besproken.
Daar lees ik dat ik xn in C kan uitrekenen met behulp van
de standaard functie pow. Vervolgens vraag ik mezelf af hoe
ik in C n! (n faculteit) uit kan rekenen. In mijn index van
mijn C boek kan ik het begrip faculteit niet vinden. Toch weet ik (omdat
ik altijd netjes mijn huiswerk maak ;-) dat het een keer in het boek ben
tegengekomen. Na enig geblader vind ik op pagina 130 het volgende voorbeeld
van het gebruik van een for lus:
for (i = 1; i <= n + 1; i = i + 1) {faculteit = faculteit * i;}
(In het boek wordt gebruik gemaakt van de verkorte schrijfwijze van enkele operatoren en zijn de accolades weggelaten.)
Als ik naar de formule kijk dan zie ik dat ik de eerste term (1) ook kan vervangen door x0/0!. Dat geeft een mooie regelmaat in de termen. Om vertrouwd te raken met de benaderingsformule reken ik de eerste 4 termen uit van cos(1.0). Deze termen zijn: 1, -12/2! = -1/(1*2) = -0.5, 14/4! = 1/(1*2*3*4) = 1/24 = 0.0416667 en -16/6! = -1/(1*2*3*4*5*6) = -1/720 = 0.0013889 De benadering van cos(1.0) met 4 termen is dus 1 + -0.5 + 0.0416667 + -0.0013889 = 0.5402778. De werkelijke waarde van cos(1.0) is volgens mijn rekenmachine: 0,5403023. Ik zie dat bij een benadering met 4 termen van cos(1.0) al 3 cijfers achter de decimale punt correct zijn.
Elk C programma heeft hetzelfde begin en einde. Ik heb een bestandje
c.c
gemaakt
waarin een C programma staat dat niets doet. Ik begin met een kopietje van
dat bestand:
#include <stdio.h>/* © 2012 Harry Broeders */int main(void) {/* Hier komt de code */fflush(stdin);getchar();return 0;}
Het is altijd handig om met de invoer te beginnen. Ik begin dus met het inlezen
van x, het floating point getal waar ik de cosinus van wil benaderen.
Omdat ik dit zo nauwkeurig mogelijk wil doen definieer ik de variabele
x van het type double. Zie eventueel
hier. Ik herinner mij uit de les dat ik een
double kan inlezen met behulp van scanf. Voordat
ik de waarde van x inlees wil ik de gebruiker eerst vertellen wat
er van hem/haar verwacht wordt door op het scherm te zetten: Geef x:
, dat kan ik doen met behulp van printf. Om te kijken
of het inlezen is gelukt druk ik de waarde van x af. Zie
cos_stap1.c:
#include <stdio.h>/* © 2012 Harry Broeders *//* benader cos(x) met de volgende formule cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ... *//* in deze formule betekent x^4: x tot de macht 4. Dat werkt niet in C. *//* in deze formule betekent 4!: 4 faculteit. Dat werkt niet in C. *//* stap 0; formule herschrijven cos(x) = x^0/0! - x^2/2! + x^4/4! - x^6/6! + ... *//* waarbij x de hoek in radialen is *//* aantal termen is een variabele die moet worden ingelezen */int main(void) {double x;printf("Geef x: ");scanf("%lf", &x);printf("cos(%f) = %f\n", x, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Als ik de waarde 1 invoer dan ziet de uitvoer van het programma er als volgt uit (de invoer is onderstreept weergegeven):
Geef x: 1 cos(1.000000) = 0.000000
Als ik de waarde -1.32 invoer dan ziet de uitvoer van het programma er als volgt uit:
Geef x: -1.32 cos(-1.320000) = 0.000000
Het aantal termen dat gebruikt moet worden om de cosinus te benaderen is variabel en moet door het programma worden ingelezen. Ik bedenk me dat het aantal termen >0 moet zijn en dat het netjes is om te controlleren of het ingevoerde getal aan deze voorwaarde voldoet. Wat moet er gebeuren als de gebruiker een getal invoert dat <=0 is? Ik besluit om de gebruiker opnieuw te vragen om de waarde in te voeren (zonder foutmelding) en de ingevoerde waarde opnieuw in te lezen. Ik wil dus het programmadeel:
printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);
herhalen totdat een geldige waarde is ingevoerd. Ik herinner me uit de les
dat er verschillende herhalingsinstructies zijn (for, do
while en while). Het bovenstaande programmadeel moet
minstens 1x herhaald worden en het is afhankelijk van de gebruiker hoe vaak
het herhaald moet worden. Het programmadeel moet dus een onbekend aantal
maal >=1 herhaald worden. Om die reden moet ik (volgens de theorieles)
kiezen voor een do while lus. Zie
cos_stap2.c:
#include <stdio.h>int main(void) {double x;int aantalTermen;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen probeer ik eerst een aantal ongeldige waarden en constateer dat het programma correct werkt:
Geef x: -1.397 Geef het aantal termen: -3 Geef het aantal termen: 0 Geef het aantal termen: 5 cos(-1.397000) benaderd met 5 termen = 0.000000
De waarde van aantalTermen wordt nu dus succesvol ingelezen
en op de juiste wijze gecontroleerd. Nu moet ik de termen van de benadering
gaan berekenen. Dit is voor een beginnend programmeur misschien te moeilijk
om in één stap uit te voeren. Ik bedenk dat het niet zo moeilijk
is om de termen te nummeren: 0, 1, 2, 3, 4, ... Dit nummer kan ik dan later
gebruiken om de verschillende onderdelen van de termen te berekenen. Ik laat
maak een variable termNummer en die krijgt achtereenvolgens
(in een herhaling) de waarde: 0, 1, 2, 3, 4, ... Het aantal herhalingen is
bekend als de herhaling begint (want de waarde van aantalTermen
is dan al ingelezen). Omdat het aantal herhalingen bekend is moet ik (volgens
de theorieles) kiezen voor een for lus. Om te testen druk ik
de waarde van de variabele termNummer voor elke term af. Zie
cos_stap3.c:
#include <stdio.h>int main(void) {double x;int aantalTermen, termNummer;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {printf("Test: termNummer = %d\n", termNummer);}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma correct werkt:
Geef x: -1.39 Geef het aantal termen: 6 Test: termNummer = 0 Test: termNummer = 1 Test: termNummer = 2 Test: termNummer = 3 Test: termNummer = 4 Test: termNummer = 5 cos(-1.390000) benaderd met 6 termen = 0.000000
Elke term gebruikt een bepaalde constante waarde. Term nummer 0 gebruikt
de constante waarde 0, term nummer 1 gebruikt de constante waarde 2, term
nummer 2 gebruikt de constante waarde 4, enz. Deze constante waarde noem
ik termConstante en deze is eenvoudig te berekenen voor elke
term met de formule: termConstante = termNummer
* 2;. Om te testen druk ik de waarde van de variabele
termConstante voor elke term af. Zie
cos_stap4.c:
#include <stdio.h>int main(void) {double x;int aantalTermen, termNummer, termConstante;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;printf("Test: termConstante = %d\n", termConstante);}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma correct werkt:
Bij het testen blijkt dat het programma correct werkt: Geef x: -1.39 Geef het aantal termen: 6 Test: termNummer = 0 Test: termNummer = 2 Test: termNummer = 4 Test: termNummer = 6 Test: termNummer = 8 Test: termNummer = 10 cos(-1.390000) benaderd met 6 termen = 0.000000
Elke term bestaat uit een breuk. Elke breuk heeft een teller (het gedeelte
boven de breukstreep) en een noemer (het gedeelte onder de breukstreep).
De tellers van de termen zijn x0, x2,
x4, x6, ... Elke term heeft dus als
teller xtermConstante. Deze waarde kan
berekend worden met de standaard functie pow. Om deze functie
te kunnen gebruiken moet ik math.h includen. Om te testen druk
ik de waarde van de teller voor elke term (variabele termTeller)
voor elke term af. Zie
cos_stap5a.c:
#include <stdio.h>#include <math.h>int main(void) {double x, termTeller;int aantalTermen, termNummer, termConstante;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;termTeller = pow(x, termConstante);printf("Test: termTeller = %f\n", termTeller);}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma correct werkt:
Geef x: 2 Geef het aantal termen: 5 Test: termTeller = 1.000000 Test: termTeller = 4.000000 Test: termTeller = 16.000000 Test: termTeller = 64.000000 Test: termTeller = 256.000000 cos(2.000000) benaderd met 5 termen = 0.000000
Op zich is dit een goede oplossing maar ik vraag me af of ik de benadering
van de cosinus ook kan bereken zonder gebruik te maken van de C math library.
Ik kijk nog eens goed naar de tellers van de termen:
x0, x2, x4,
x6, x8, ... Deze termen kan ik ook
als volgt schrijven: x0, x0 *
x2, x2 * x2,
x4 * x2, x6 *
x2, ... Als ik een teller heb berekend dan kan ik de volgende
teller berekenen door de laatst berekende teller te vermenigvuldigen met
x2. Als ik x2 uitrekenen als x
* x dan heb ik met deze aanpak de pow functie niet meer
nodig. Zie
cos_stap5b.c:
#include <stdio.h>int main(void) {double x, termTeller;int aantalTermen, termNummer, termConstante;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;printf("Test: termTeller = %f\n", termTeller);/* bereken volgende termTeller */termTeller = termTeller * x * x;}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma (nog steeds) correct werkt:
Geef x: 2 Geef het aantal termen: 5 Test: termTeller = 1.000000 Test: termTeller = 4.000000 Test: termTeller = 16.000000 Test: termTeller = 64.000000 Test: termTeller = 256.000000 cos(2.000000) benaderd met 5 termen = 0.000000
Elke term bestaat uit een breuk. Elke breuk heeft een teller (het gedeelte
boven de breukstreep) en een noemer (het gedeelte onder de breukstreep).
De noemers van de termen zijn 0!, 2!, 4!, 6!, ... Elke term heeft dus als
noemer termConstante! (de faculteit van de
termConstante). De waarde van n! kan berekend worden
als 1 * 2 * 3 * 4 * .... n. Omdat het aantal vermenigvuldingen voor
een bepaalde waarde van n bekend is (namelijk n) kun je een
eenvoudige for lus gebruiken om n! uit te rekenen:
n_fac = 1;for (i = 2; i <= n; i = i + 1) {n_fac = n_fac * i;}
De waarde van n! groeit heel snel. De waarde van 13! past al niet
meer in een variabele van het type int (een 32 bits two's complement
getal). Om deze reden definiëren we de variabele termNoemer
van het type double. Om te testen druk ik de waarde van de noemer
voor elke term (variabele termNoemer) voor elke term af. Zie
cos_stap6a.c:
#include <stdio.h>int main(void) {double x, termTeller, termNoemer;int aantalTermen, termNummer, termConstante, i;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;termNoemer = 1;for (i = 2; i <= termConstante; i = i + 1) {termNoemer = termNoemer * i;}printf("Test: termNoemer = %f\n", termNoemer);/* bereken volgende termTeller */termTeller = termTeller * x * x;}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma correct werkt:
Geef x: 1.52 Geef het aantal termen: 5 Test: termNoemer = 1.000000 Test: termNoemer = 2.000000 Test: termNoemer = 24.000000 Test: termNoemer = 720.000000 Test: termNoemer = 40320.000000 cos(1.520000) benaderd met 5 termen = 0.000000
Op zich is dit een goede oplossing maar ik vraag me af of ik de waarde van
termNoemer ( = termConstante!) tekens opnieuw uit
moet rekenen. Ik kijk nog eens goed naar de noemers van de termen: 0!, 2!,
4!, 6!, 8! ... Deze termen kan ik ook als volgt schrijven: 0!, 0! *
1 * 2, 2! * 3 * 4, 4! * 5 * 6, 6! * 7 * 8, ... Als ik een noemer heb berekend
dan kan ik de volgende noemer berekenen door de laatst berekende noemer (met
de waarde termConstante!) te vermenigvuldigen met
(termConstante + 1) * (termConstante + 2). Zie
cos_stap6b.c:
#include <stdio.h>int main(void) {double x, termTeller, termNoemer;int aantalTermen, termNummer, termConstante;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;termNoemer = 1;for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;printf("Test: termNoemer = %f\n", termNoemer);/* bereken volgende termTeller */termTeller = termTeller * x * x;/* bereken volgende termNoemer */termNoemer = termNoemer * (termConstante + 1) * (termConstante + 2);}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma (nog steeds) correct werkt:
Geef x: 1.52 Geef het aantal termen: 5 Test: termNoemer = 1.000000 Test: termNoemer = 2.000000 Test: termNoemer = 24.000000 Test: termNoemer = 720.000000 Test: termNoemer = 40320.000000 cos(1.520000) benaderd met 5 termen = 0.000000
Elke term heeft een teken. Het teken is afwisseld positief en negatief dus:
+1, -1, +1, -1, +1, ... Als je dus het teken van een term kent dan kun je
het teken van de volgende term berekenen door het bekende teken te
vermenigvuldigen met -1. Om te testen druk ik het teken voor elke term (variabele
termTeken) voor elke term af. Zie
cos_stap7.c:
#include <stdio.h>int main(void) {double x, termTeller, termNoemer;int aantalTermen, termNummer, termConstante, termTeken;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;termNoemer = 1;termTeken = 1;for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;printf("Test: termTeken = %d\n", termTeken);/* bereken volgende termTeller */termTeller = termTeller * x * x;/* bereken volgende termNoemer */termNoemer = termNoemer * (termConstante + 1) * (termConstante + 2);/* bereken volgende termTeken */termTeken = termTeken * -1;}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma correct werkt:
Geef x: -1.23 Geef het aantal termen: 7 Test: termTeken = 1 Test: termTeken = -1 Test: termTeken = 1 Test: termTeken = -1 Test: termTeken = 1 Test: termTeken = -1 Test: termTeken = 1 cos(-1.230000) benaderd met 7 termen = 0.000000
We hebben nu de teller, de noemer en het teken van elke term berekend. Het
is nu eenvoudig om de waarde van elke term te berekenen: term = termTeken
* termTeller / termNoemer. Zie
cos_stap8.c:
#include <stdio.h>int main(void) {double x, termTeller, termNoemer, term;int aantalTermen, termNummer, termConstante, termTeken;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;termNoemer = 1;termTeken = 1;for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;term = termTeken * termTeller / termNoemer;printf("Test: term = %f\n", term);/* bereken volgende termTeller */termTeller = termTeller * x * x;/* bereken volgende termNoemer */termNoemer = termNoemer * (termConstante + 1) * (termConstante + 2);/* bereken volgende termTeken */termTeken = termTeken * -1;}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, 0); /* dit is nog niet het goede antwoord! */fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma de eerste 4 termen van cos(1) correct berekent (ik heb de uitkomsten vergeleken met de in stap 0 met behulp van de rekenmachine berekende waarden):
Geef x: 1 Geef het aantal termen: 4 Test: term = 1.000000 Test: term = -0.500000 Test: term = 0.041667 Test: term = -0.001389 cos(1.000000) benaderd met 4 termen = 0.000000
We kunnen nu de benadering van de cosinus eenvoudig berekenen door alle berekende
termen bij elkaar op te tellen. Zie
cos_stap9.c:
#include <stdio.h>int main(void) {double x, termTeller, termNoemer, term, cos;int aantalTermen, termNummer, termConstante, termTeken;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;termNoemer = 1;termTeken = 1;cos = 0;for (termNummer = 0; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;term = termTeken * termTeller / termNoemer;cos = cos + term;/* bereken volgende termTeller */termTeller = termTeller * x * x;/* bereken volgende termNoemer */termNoemer = termNoemer * (termConstante + 1) * (termConstante + 2);/* bereken volgende termTeken */termTeken = termTeken * -1;}printf("cos(%f) benaderd met %d termen = %f\n", x, aantalTermen, cos);fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma de eerste 4 termen van cos(1) correct optelt (ik heb de uitkomst vergeleken met de in stap 0 met behulp van de rekenmachine berekende waarde):
Geef x: 1 Geef het aantal termen: 4 cos(1.000000) benaderd met 4 termen = 0.540278
Als ik nog eens goed naar het bovenstaande programma kijk dan zie ik dat
het helemaal niet zo handig is om term 0 in de for lus uit te
rekenen. Het is veel eenvoudiger om gewoon te beginnen met term 0 (die altijd
de waarde 1 heeft). Verder druk ik het antwoord met 15 decimalen na de punt
af zodat ik kan zien of de benadering nauwkeurig genoeg is. Een double heeft
minimaal 15 en maximaal 17 significante cijfers dus meer cijfers achter de
punt afdrukken is zinloos, zie eventueel hier.
Uiteindelijk kom ik dus tot het volgende programma, zie
cos_stap10.c :
#include <stdio.h>int main(void) {double x, termTeller, termNoemer, term, cos;int aantalTermen, termNummer, termConstante, termTeken;printf("Geef x: ");scanf("%lf", &x);do {printf("Geef het aantal termen: ");scanf("%d", &aantalTermen);} while (aantalTermen <= 0);termTeller = 1;termNoemer = 1;termTeken = 1;cos = 1;for (termNummer = 1; termNummer < aantalTermen; termNummer = termNummer + 1) {termConstante = termNummer * 2;termTeller = termTeller * x * x;termNoemer = termNoemer * (termConstante - 1) * termConstante;termTeken = termTeken * -1;term = termTeken * termTeller / termNoemer;cos = cos + term;}printf("cos(%f) benaderd met %d termen = %.15f\n", x, aantalTermen, cos);fflush(stdin);getchar();return 0;}
Bij het testen blijkt dat het programma de cosinus correct benaderd. De waarde van cos(0.5) is 0.8775825618903727 volgens mijn rekenmachine. Als we cos(0.5) met 6 termen berekenen dan is het antwoord tot op 10 cijfers achter de punt correct. Als we 7 termen gebruiken dan zijn alle afgedrukte 15 cijfers achter de punt correct:
Geef x: 0.5 Geef het aantal termen: 6 cos(0.500000) benaderd met 6 termen = 0.877582561889864 Geef x: 0.5 Geef het aantal termen: 7 cos(0.500000) benaderd met 7 termen = 0.877582561890373