Uitleg over alpha-beta pruning (SOPX3 en SYSO1).

Deze pagina is bestemd voor studenten van de THRijswijk groep EH3 C&D en IH3 SYSO.

Min-max algoritme.

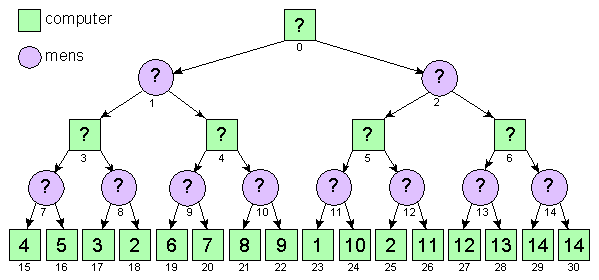
Als je de beste zet in een spel (met 2 spelers, die elk afwisselend aan de beurt zijn) wilt vinden kun een boom tekenen met alle mogelijke posities. Stel dat deze boom er (voor een denkbeeldig spel) als volgt uitziet:

In deze figuur is een vierkant getekend voor een positie waarbij de computer aan de beurt is en een rondje als de tegenstander (mens) aan de beurt is. De waarde van een positie is 15 als de computer wint en 0 als de mens wint. De computer moet dus een positie met een zo hoog mogelijke waarde zien te bereiken.

De posities zijn genummerd van boven naar beneden en van links naar rechts. Voor elke positie 15<=p<31 geldt dat de waarde van deze positie bekend is. Voor elke positie 0<=p<15 geldt dat de twee mogelijke volgende posities p*2+1 en p*2+2 zijn. Bijvoorbeeld: positie 4 heeft als mogelijke volgende posities 9 (2*4+1) en 10 (2*4+2).

De computer moet de hoogst haalbare waarde zien te bereiken. In de figuur lijkt dit een van de twee posities met de waarde 14 maar deze zijn onbereikbaar denk maar even na. Bij zijn eerste beurt gaat de computer naar rechts (richting 14). De tegenstander (mens) zal dan echter naar links gaan. De computer zal nu bij zijn volgende beurt naar rechts gaan (richting 11) maar zijn tegenstander zal bij de volgende beurt weer voor links kiezen waardoor de bereikte positie de waarde 2 heeft (niet best voor de computer dus).

Is dit de hoogst haalbare waarde voor de computer?

De hoogst haalbare waarde kan bepaald worden door van onder naar boven door de boom te wandelen en de waarde van elk knooppunt als volgt te bepalen:

Als de computer aan de beurt is moet je voor de positie kiezen met de hoogste waarde (de computer wil zo sterk mogelijk spelen).
Als de mens aan de beurt is (de tegenstander) moet je voor de positie kiezen met de laagste waarde (er van uitgaande dat de tegenstander zo sterk mogelijk speelt).

Omdat je dus afwisselend kiest voor de maximale (als de computer aan de beurt is) en de minimale (als de tegenstander aan de beurt is) waarde wordt dit algoritme het min-max algoritme genoemd.

In het onderstaande programma MinMax0.cpp wordt de boom uit de bovenstaande tekening gebruikt en wordt de hoogst haalbare waarde berekend met het het min-max algoritme. Er wordt daarbij gebruik gemaakt van 2 functies die elkaar (recursief) aanroepen.

#include <iostream>
#include <iomanip>
using namespace std;

int positionValue(int pos);
void printTree(int pos, int level);
int valueMoveComputer(int pos);
int valueMoveHuman(int pos);

int positionValue(int pos) {
    static const int value[16]={4,5,3,2,6,7,8,9,1,10,2,11,12,13,14,14};
    if (pos>=15 && pos<31)
        return value[pos-15];
    return -1;
}

int valueMoveComputer(int pos) {
    int value(positionValue(pos));
    if (value==-1) {
        value=0;
        for (int i(1); i<3; ++i) {
            int reply(valueMoveHuman(2*pos+i));
            if (reply>value) {
                value=reply;
            }
        }
    }
    return value;
}

int valueMoveHuman(int pos) {
    int value(positionValue(pos));
    if (value==-1) {
        value=15;
        for (int i(1); i<3; ++i) {
            int reply(valueMoveComputer(2*pos+i));
            if (reply<value) {
                value=reply;
            }
        }
    }
    return value;
}

int main() {
    cout<<"Pos:  0"<<" Value: "<<setw(2)<<valueMoveComputer(0)<<endl;
    for (int p(1); p<3; ++p)
        cout<<"Pos: "<<setw(2)<<p
            <<" Value: "<<setw(2)<<valueMoveHuman(p)<<endl;
    for (int p(3); p<7; ++p)
        cout<<"Pos: "<<setw(2)<<p
            <<" Value: "<<setw(2)<<valueMoveComputer(p)<<endl;
    for (int p(7); p<15; ++p)
        cout<<"Pos: "<<setw(2)<<p
            <<" Value: "<<setw(2)<<valueMoveHuman(p)<<endl;
    cin.get();
}

De functie positionValue geeft -1 terug als de waarde van de positie berekend moet worden. Als de positie zich in de onderste laag van de boom bevindt en de waarde dus bekend is, geeft positionValue deze waarde terug.

De functie valueMoveComputer wordt aangeroepen om te bepalen wat de waarde van de positie pos is als de computer aan de beurt is in deze positie. Deze functie moet dus het maximum bepalen van de (in dit geval twee) posities die vanuit de positie pos bereikt kunnen worden. In deze binaire boom zijn dat de posities: 2*pos+1 en 2*pos+2. Bij binnenkomst van de functie valueMoveComputer wordt eerst de functie positionValue aangeroepen. De returnwaarde van deze functie wordt opgeslagen in de lokale variabele value. Als de waarde van value ongelijk is aan -1 kan de functie valueMoveComputer deze waarde meteen teruggeven. De positie pos bevindt zich in dat geval in de onderste laag van de boom. Als de positie pos waarmee de functie valueMoveComputer is aangeroepen zich niet in de onderste laag van de boom bevindt geeft de functie positionValue de waarde -1 terug en wordt de waarde van de variabele value gelijk gemaakt aan het absolute minimum (in dit geval 0). Het is logisch dat een functie die het maximum moet bepalen begint met het (tot dan toe gevonden) maximum gelijk te maken aan het absolute minimum. Vervolgens wordt in de for lus de waarde van de (in dit geval twee) posities die vanuit de positie pos bereikt kunnen worden bepaald. Dit gebeurt door het aanroepen van de functie valueMoveHuman met als argument 2*pos+i waarbij i achtereenvolgens de waarde 1 en 2 heeft. We moeten hier de functie valueMoveHuman aanroepen omdat als in positie pos de computer aan de beurt is, in de posities die vanuit de positie pos bereikt kunnen worden de tegenstander (mens) aan de beurt zal zijn. De returnwaarde van deze functie wordt opgeslagen in de lokale variabele reply. Als de waarde van reply groter is dan het tot nu toe gevonden maximum (opgeslagen in de variabele value) dan wordt het tot nu toe gevonden maximum gelijk gemaakt aan reply. Aan het einde van de for lus zal de variabele value dus het maximum bevatten van de (in dit geval twee) posities die vanuit de positie pos bereikt kunnen worden. De waarde van value wordt teruggegeven aan de aanroepende functie.

De functie valueMoveHuman wordt aangeroepen als de mens aan de beurt is en lijkt erg veel op de functie valueMoveComputer, in plaats van het maximum wordt echter het minimum bepaald.

De functie valueMoveHuman wordt aangeroepen om te bepalen wat de waarde van de positie pos is als de mens aan de beurt is in deze positie. Deze functie moet dus het minimum bepalen van de (in dit geval twee) posities die vanuit de positie pos bereikt kunnen worden. In deze binaire boom zijn dat de posities: 2*pos+1 en 2*pos+2. Bij binnenkomst van de functie valueMoveHuman wordt eerst de functie positionValue aangeroepen. De returnwaarde van deze functie wordt opgeslagen in de lokale variabele value. Als de waarde van value ongelijk is aan -1 kan de functie valueMoveHuman deze waarde meteen teruggeven. De positie pos bevindt zich in dat geval in de onderste laag van de boom. Als de positie pos waarmee de functie valueMoveHuman is aangeroepen zich niet in de onderste laag van de boom bevindt geeft de functie positionValue de waarde -1 terug en wordt de waarde van de variabele value gelijk gemaakt aan het absolute maximum (in dit geval 15). Het is logisch dat een functie die het minimum moet bepalen begint met het (tot dan toe gevonden) minimum gelijk te maken aan het absolute maximum. Vervolgens wordt in de for lus de waarde van de (in dit geval twee) posities die vanuit de positie pos bereikt kunnen worden bepaald. Dit gebeurt door het aanroepen van de functie valueMoveComputer met als argument 2*pos+i waarbij i achtereenvolgens de waarde 1 en 2 heeft. We moeten hier de functie valueMoveComputer aanroepen omdat als in positie pos de mens aan de beurt is, in de posities die vanuit de positie pos bereikt kunnen worden de computer aan de beurt zal zijn. De returnwaarde van deze functie wordt opgeslagen in de lokale variabele reply. Als de waarde van reply kleiner is dan het tot nu toe gevonden minimum (opgeslagen in de variabele value) dan wordt het tot nu toe gevonden minimum gelijk gemaakt aan reply. Aan het einde van de for lus zal de variabele value dus het minimum bevatten van de (in dit geval twee) posities die vanuit de positie pos bereikt kunnen worden. De waarde van value wordt teruggegeven aan de aanroepende functie.

In de functie main wordt ervan uitgegaan dat de computer in positie 0 aan de beurt is. In de volgende laag van de boom (posities 1 en 2) zal dus de mens aan de beurt zijn enz. Er vanuitgaande dat de computer in positie 0 aan de beurt is worden de waarden van alle posities in de boom bepaald en afgedrukt. De uitvoer van dit programma is:

Pos:  0 Value:  4
Pos:  1 Value:  4
Pos:  2 Value:  2
Pos:  3 Value:  4
Pos:  4 Value:  8
Pos:  5 Value:  2
Pos:  6 Value: 14
Pos:  7 Value:  4
Pos:  8 Value:  2
Pos:  9 Value:  6
Pos: 10 Value:  8
Pos: 11 Value:  1
Pos: 12 Value:  2
Pos: 13 Value: 12
Pos: 14 Value: 14

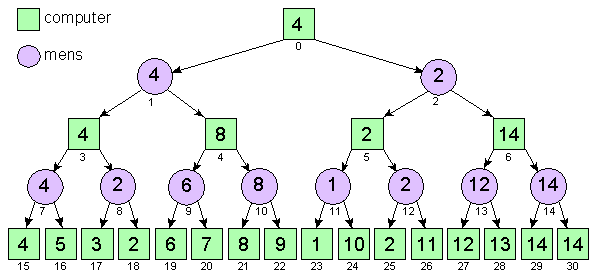
In de bovenstaande figuur kun je zien dat met behulp van het min-max algoritme de best bereikbare positie voor de computer wordt gevonden.

Het is ook mogelijk om de functies valueMoveComputer en valueMoveHuman te combineren tot 1 functie:

enum Side {HUMAN, COMPUTER};

int valueMove(Side s, int pos) {
    int value(positionValue(pos));
    if (value==-1) {
        value=(s==COMPUTER)?0:15;
        for (int i(1); i<3; ++i) {
            int reply(valueMove((s==COMPUTER)?HUMAN:COMPUTER, 2*pos+i));
            if (s==COMPUTER&&reply>value || s==HUMAN&&reply<value) {
                value=reply;
            }
        }
    }
    return value;
}

Er zijn echter 2 redenen om dit niet te doen:

De functie wordt moeilijker te begrijpen en dus moeilijker te debuggen en/of aan te passen.
Het programma wordt minder snel (omdat steeds extra condities moeten worden bepaald). In de praktijk wordt het min-max algoritme gebruikt voor spelletjes waarbij het aantal door te rekenen posities veel groter is dan in dit voorbeeld. Snelheid is dan belangrijk.

In het bovenstaande programma wordt alleen de waarde van de positie bepaald. Dit is uiterraard niet voldoende. We moeten ook weten welke zet we moeten doen om deze waarde te bereiken! Dit kan "eenvoudig" worden bereikt door bij het zoeken naar de maximale of minimale waarde de beste positie te onthouden in de lokale variabele bestNextPos en aan het einde van de functie terug te geven. Omdat een functie echter maar één variabele kan teruggeven is het noodzakelijk om de twee returnwaarden (de waarde van de positie en de beste volgende positie) in te pakken in een standaard pair<int, int> object.

#include <iostream>
#include <iomanip>
using namespace std;

int positionValue(int pos);
pair<int, int> chooseMoveComputer(int pos);
pair<int, int> chooseMoveHuman(int pos);

int positionValue(int pos) {
    static const int value[16]={4,5,3,2,6,7,8,9,1,10,2,11,12,13,14,14};
    if (pos>=15 && pos<31)
        return value[pos-15];
    return -1;
}

pair<int, int> chooseMoveComputer(int pos) {
    int value(positionValue(pos));
    int bestNextPos(pos);
    if (value==-1) {
        value=0;
        for (int i(1); i<3; ++i) {
            pair<int, int> reply(chooseMoveHuman(2*pos+i));
            if (reply.first>value) {
                value=reply.first;
                bestNextPos=2*pos+i;
            }
        }
    }
    return make_pair(value, bestNextPos);
}

pair<int, int> chooseMoveHuman(int pos) {
    int value(positionValue(pos));
    int bestNextPos(pos);
    if (value==-1) {
        value=15;
        for (int i(1); i<3; ++i) {
            pair<int, int> reply(chooseMoveComputer(2*pos+i));
            if (reply.first<value) {
                value=reply.first;
                bestNextPos=2*pos+i;
            }
       }
    }
    return make_pair(value, bestNextPos);
}

int main() {
    pair<int, int> res(chooseMoveComputer(0));
    cout<<"Pos:  0"
        <<" Value: "<<setw(2)<<res.first
        <<" BestPos: "<<setw(2)<<res.second<<endl;
    for (int p(1); p<3; ++p) {
        res=chooseMoveHuman(p);
        cout<<"Pos: "<<setw(2)<<p
            <<" Value: "<<setw(2)<<res.first
            <<" BestPos: "<<setw(2)<<res.second<<endl;
    }
    for (int p(3); p<7; ++p) {
        res=chooseMoveComputer(p);
        cout<<"Pos: "<<setw(2)<<p
            <<" Value: "<<setw(2)<<res.first
            <<" BestPos: "<<setw(2)<<res.second<<endl;
    }
    for (int p(7); p<15; ++p) {
        res=chooseMoveHuman(p);
        cout<<"Pos: "<<setw(2)<<p
            <<" Value: "<<setw(2)<<res.first
            <<" BestPos: "<<setw(2)<<res.second<<endl;
    }
    cin.get();
}

De uitvoer van dit programma MinMax1.cpp is als volgt:

Pos:  0 Value:  4 BestPos:  1
Pos:  1 Value:  4 BestPos:  3
Pos:  2 Value:  2 BestPos:  5
Pos:  3 Value:  4 BestPos:  7
Pos:  4 Value:  8 BestPos: 10
Pos:  5 Value:  2 BestPos: 12
Pos:  6 Value: 14 BestPos: 14
Pos:  7 Value:  4 BestPos: 15
Pos:  8 Value:  2 BestPos: 18
Pos:  9 Value:  6 BestPos: 19
Pos: 10 Value:  8 BestPos: 21
Pos: 11 Value:  1 BestPos: 23
Pos: 12 Value:  2 BestPos: 25
Pos: 13 Value: 12 BestPos: 27
Pos: 14 Value: 14 BestPos: 29

Alpha-beta pruning.

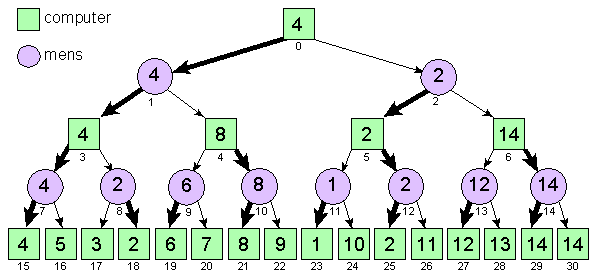
Bij het zoeken naar een minimale waarde op een bepaalde positie kun je stoppen zodra je een waarde hebt gevonden die kleiner of gelijk is aan de tot dan toe gevonden maximale waarde in de bovenliggende positie.

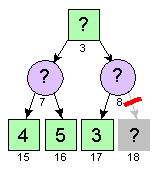
In de bovenstaande figuur is de waarde van positie 3 gelijk aan het maximum van de waarden van de posities 7 en 8. De waarde van positie 7 is het minimum van de waarden van de posities 15 en 16. De waarde van positie 7 is dus 4 (het minimum van 4 en 5). Het tijdelijke maximum in positie 3 wordt dus (na het berekenen van de waarde van positie 7) gelijk gemaakt aan 4. De waarde van positie 8 is het minimum van positie 17 en 18. Bij het zoeken naar dit minimum wordt eerst de waarde 3 voor positie 17 gevonden. Omdat deze waarde kleiner of gelijk is aan het tot nu toe gevonden maximum in de bovenliggende positie (de waarde 4) kunnen we meteen stoppen! Het is dus niet nodig om de waarde van positie 18 te bepalen. Denk maar mee. Als deze waarde <3 (b.v. 0) is dan wordt deze waarde gekozen als minimale waarde. Echter in de bovenliggende positie (positie 3) wordt toch voor de maximale waarde 4 gekozen. Als de waarde van positie 18 >3 (b.v. 15) is dan wordt de waarde 3 (van positie 17) gekozen als minimale waarde. Echter in de bovenliggende positie (positie 3) wordt toch voor de maximum waarde 4 gekozen. De waarde van positie 18 hoeft dus helemaal niet bepaald te worden. Dit deel van de boom hoeft niet "doorzocht" te worden en we kunnen als het ware de zoekboom snoeien (Engels: to prune). Om dit mogelijk te maken moet wel de tot dan toe gevonden maximale waarde van de bovenliggende positie worden doorgegeven aan de onderliggende posities. Dit gebreurt in het onderstaande programma door middel van de parameter alpha. Deze naam is toevallig zo gekozen door de bedenkers van dit algoritme en heeft verder geen betekenis.

Bij het zoeken naar een maximale waarde op een bepaalde positie kun je stoppen zodra je een waarde hebt gevonden die groter of gelijk is aan de tot dan toe gevonden minimale waarde in de bovenliggende positie.

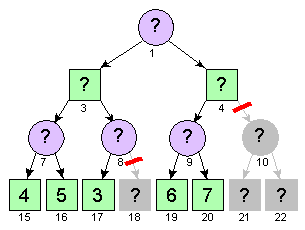
In de bovenstaande figuur is de waarde van positie 1 gelijk aan het minimum van de waarden van de posities 3 en 4. De waarde van positie 3 is hiervoor al bepaald (4). Het tijdelijke minimum in positie 1 wordt dus (na het berekenen van de waarde van positie 3) gelijk gemaakt aan 4. De waarde van positie 4 is het maximum van positie 9 en 10. Bij het zoeken naar dit maximum wordt eerst de waarde 6 voor positie 9 gevonden (door het minimum te bepalen van positie 19 en 20). Omdat het tot nu toe gevonden maximum in positie 4 (de waarde 6) groter of gelijk is aan het tot nu toe gevonden minimum in de bovenliggende positie (de waarde 4) kunnen we meteen stoppen! Het is dus niet nodig om de waarden van posities 10, 21 en 22 te bepalen. Denk maar mee. Als de waarde van positie 10 >6 (b.v. 15) is dan wordt deze waarde gekozen als maximale waarde. Echter in de bovenliggende positie (positie 1) wordt toch als minimale waarde 4 gekozen. Als de waarde van positie 10 <6 (b.v. 0) is dan wordt de waarde 6 (van positie 9) gekozen als maximale waarde. Echter in de bovenliggende positie (positie 1) wordt toch als minimale waarde 4 gekozen. De waarden van posities 10, 21 en 22 hoeven dus helemaal niet bepaald te worden. Dit deel van de boom hoeft niet "doorzocht" te worden en we kunnen de zoekboom weer snoeien. Om dit mogelijk te maken moet wel de tot dan toe gevonden minimale waarde van de bovenliggende positie worden doorgegeven aan de onderliggende posities. Dit gebreurt in het onderstaande programma AlphaBeta0.cpp door middel van de parameter beta. Deze naam is toevallig zo gekozen door de bedenkers van dit zogenaamde alpha-beta pruning algoritme en heeft verder geen betekenis. Het alpha-beta algoritme is in 1958 bedacht door 3 wetenschappers van de Carnegie-Mellon University (Allen Newell, John Shaw, en Herbert Simon).

#include <iostream>
#include <iomanip>
using namespace std;

int positionValue(int pos);
int valueMoveComputer(int pos, int alpha, int beta);
int valueMoveHuman(int pos, int alpha, int beta);

int positionValue(int pos) {
    static const int value[16]={4,5,3,2,6,7,8,9,1,10,2,11,12,13,14,14};
    if (pos>=15 && pos<31)
        return value[pos-15];
    return -1;
}

int valueMoveComputer(int pos, int alpha, int beta) {
    cout<<"pos = "<<setw(2)<<pos
        <<" alpha = "<<setw(2)<<alpha
        <<" beta = "<<setw(2)<<beta<<endl;
    int value(positionValue(pos));
    if (value==-1) {
        value=alpha;
        for (int i(1); i<3 && value<beta; ++i) {
            int reply(valueMoveHuman(2*pos+i, alpha, beta));
            if (reply>value) {
                value=reply;
                alpha=value;
            }
        }
    }
    return value;
}

int valueMoveHuman(int pos, int alpha, int beta) {
    cout<<"pos = "<<setw(2)<<pos
        <<" alpha = "<<setw(2)<<alpha
        <<" beta = "<<setw(2)<<beta<<endl;
    int value(positionValue(pos));
    if (value==-1) {
        value=beta;
        for (int i(1); i<3 && value>alpha; ++i) {
            int reply(valueMoveComputer(2*pos+i, alpha, beta));
            if (reply<value) {
                value=reply;
                beta=value;
            }
        }
    }
    return value;
}

int main() {
    cout<<"Pos:  0"
        <<" Value: "<<setw(2)<<valueMoveComputer(0, 0, 15)<<endl;
    cin.get();
}

De uitvoer van dit programma is als volgt:

pos =  0 alpha =  0 beta = 15
pos =  1 alpha =  0 beta = 15
pos =  3 alpha =  0 beta = 15
pos =  7 alpha =  0 beta = 15
pos = 15 alpha =  0 beta = 15
pos = 16 alpha =  0 beta =  4
pos =  8 alpha =  4 beta = 15
pos = 17 alpha =  4 beta = 15
pos =  4 alpha =  0 beta =  4
pos =  9 alpha =  0 beta =  4
pos = 19 alpha =  0 beta =  4
pos = 20 alpha =  0 beta =  4
pos =  2 alpha =  4 beta = 15
pos =  5 alpha =  4 beta = 15
pos = 11 alpha =  4 beta = 15
pos = 23 alpha =  4 beta = 15
pos = 12 alpha =  4 beta = 15
pos = 25 alpha =  4 beta = 15
Pos:  0 Value:  4

Door de extra output naar cout aan het begin van de functies valueMoveComputer en valueMoveHuman kunnen we het gedrag van dit algoritme goed volgen. Doordat de posities 6, 10, 13, 14, 18, 21, 22, 24, 26, 27, 28, 29 en 30 niet in de uitvoer voorkomen blijkt dat deze posities "gesnoeid" zijn. Zie onderstaand figuur:

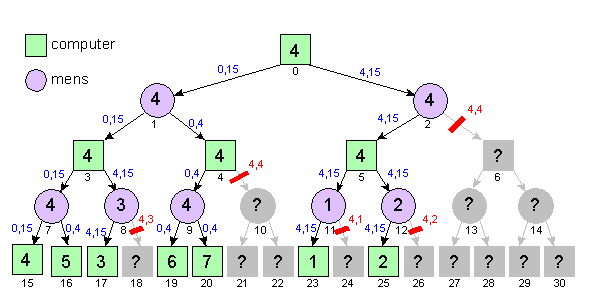
Bij de eerste aanroep van de functie valueMoveComputer moet voor alpha het absolute minimum (in dit geval 0) en voor beta het absolute maximum (in dit geval 15) worden ingevuld. Dit is logisch want alpha is het tot nu toe gevonden maximum in de bovenliggende posities (we hebben in dit geval geen bovenliggende posities dus het tot nu toe gevonden maximum is het absolute minimum) en beta is het tot nu toe gevonden minimum in de bovenliggende posities (we hebben in dit geval geen bovenliggende posities dus het tot nu toe gevonden minimum is het absolute maximum).

Je ziet dat bij het bepalen van de maximale waarde in een positie de waarde van value wordt geïnitialiseerd met alpha en niet met het absolute minimum (0). Een, in een bovenliggende positie gevonden, tijdelijk maximum mag namelijk niet in een (2 lagen dieper) onderliggende positie op een lagere waarde worden gezet! Als je value initialiseerd met 0 wordt de positie 26 niet gesnoeid! Probeer maar.

Om dezelfde reden moet bij het bepalen van de minimale waarde in een positie de waarde van value worden geïnitialiseerd met beta en niet met het absolute maximum (15). Een, in een bovenliggende positie gevonden, tijdelijk minimum mag namelijk niet in een (2 lagen dieper) onderliggende positie op een hogere waarde worden gezet!

In het bovenstaande programma wordt alleen de waarde van de positie bepaald. Dit is uiterraard niet voldoende. We moeten ook weten welke zet we moeten doen om deze waarde te bereiken! Dit kan weer worden bereikt door bij het zoeken naar de maximale of minimale waarde de beste positie te onthouden in de lokale variabele bestNextPos en aan het einde van de functie terug te geven. De twee returnwaarden (de waarde van de positie en de beste volgende positie) worden weer ingepakt in een standaard pair<int, int> object.

#include <iostream>
#include <iomanip>
using namespace std;

int positionValue(int pos);
pair<int, int> chooseMoveComputer(int pos, int alpha, int beta);
pair<int, int> chooseMoveHuman(int pos, int alpha, int beta);

int positionValue(int pos) {
    static const int value[16]={4,5,3,2,6,7,8,9,1,10,2,11,12,13,14,14};
    if (pos>=15 && pos<31)
        return value[pos-15];
    return -1;
}

pair<int, int> chooseMoveComputer(int pos, int alpha, int beta) {
    int value(positionValue(pos));
    int bestNextPos(pos);
    if (value==-1) {
        value=alpha;
        for (int i(1); i<3 && value<beta; ++i) {
            pair<int, int> reply(chooseMoveHuman(2*pos+i, alpha, beta));
            if (reply.first>value) {
                value=reply.first;
                alpha=value;
                bestNextPos=2*pos+i;
            }
        }
    }
    return make_pair(value, bestNextPos);
}

pair<int, int> chooseMoveHuman(int pos, int alpha, int beta) {
    int value(positionValue(pos));
    int bestNextPos(pos);
    if (value==-1) {
        value=beta;
        for (int i(1); i<3 && value>alpha; ++i) {
            pair<int, int> reply(chooseMoveComputer(2*pos+i, alpha, beta));
            if (reply.first<value) {
                value=reply.first;
                beta=value;
                bestNextPos=2*pos+i;
            }
        }
    }
    return make_pair(value, bestNextPos);
}

int main() {
    pair<int, int> res(chooseMoveComputer(0, 0, 15));
    cout<<"Pos:  0"
        <<" Value: "<<setw(2)<<res.first
        <<" BestPos: "<<setw(2)<<res.second<<endl;
    cin.get();
}

Uitvoer van dit programma AlphaBeta1.cpp :

Pos:  0 Value:  4 BestPos:  1

Pfff... Ik snap het!

Jullie ook? Reacties zijn altijd welkom mailto:bd.hhs.nl

Uitleg over alpha-beta pruning (SOPX3 en SYSO1).

Min-max algoritme.

Alpha-beta pruning.

Pfff... Ik snap het!

Links: